I termini “gaussiana”, “distribuzione normale” o “campana di Gauss” sono probabilmente noti anche a chi non ha fatto studi matematici o statistici. Qualora non richiamassero nulla, nemmeno alla mente del lettore, quasi certamente si avvertirà una certa familiarità con la curva a forma di campana descritta nel grafico che la rappresenta. Il motivo è da ricercarsi nell’ampio spettro di utilizzo di questo strumento, in vari campi della conoscenza umana. Si va dalla fisica alla demografia, dall’estimo alla logistica, dalla biologia all’economia, dalla medicina all’astronomia, dalla psicologia alle scienze motorie, dalla finanza alla gestione aziendale. In ogni caso, anche chi osserva per la prima volta il grafico a campana, comprende rapidamente le sue caratteristiche principali: esiste una contrapposizione tra il centro della campana e i suoi estremi e la sua forma ha una perfetta simmetria.
I primi studi sulla funzione che descrive l’andamento della densità di probabilità associata alla distribuzione normale furono quelli del matematico francese Abraham De Moivre (1733), padre della formula che porta il suo nome e che permette di esprimere la potenza di un numero complesso in forma trigonometrica. De Moivre fu il primo ad accorgersi che la già conosciuta distribuzione binomiale di probabilità, nel caso di un campione molto numeroso, assumeva una forma a campana. Fu però il matematico, astronomo e fisico tedesco Carl Friedrich Gauss che, nel 1809, ricavò la formula di tale distribuzione nell’ambito dei suoi studi sulle curve di errore nelle traiettorie degli asteroidi. Questa scoperta valse a Gauss l’imperitura memoria, tanto che – in epoche più recenti – la Bundesbank utilizzò il suo ritratto, la funzione matematica da lui utilizzata e il relativo grafico, come effigi per le banconote da 10 marchi circolanti in Germania fino all’entrata in vigore dell’euro.
Né De Moivre, né Gauss utilizzarono mai il termine “normale” per riferirsi alla distribuzione a campana oggetto dei loro studi. Il merito di aver fatto diventare quell’andamento sinonimo di “normalità” e di aver quindi allargato al concetto di “consuetudine” e di “conforme alla media”, il significato di quell’aggettivo va all’astronomo e statistico belga Adolphe Quetelet, che decise di applicare i criteri con cui venivano effettuate le misurazioni astronomiche allo studio dell’essere umano e della società. Fino a circa il 1850, la “norma” non era altro che uno strumento – tuttora esistente – utilizzato nel campo delle misurazioni, che serviva a stabilire la “rettitudine” di un angolo. Quetelet realizzò statistiche sulle caratteristiche umane più disparate ed è a lui che dobbiamo la nascita dell’idea attuale di normalità relativa all’individuo e alla società.
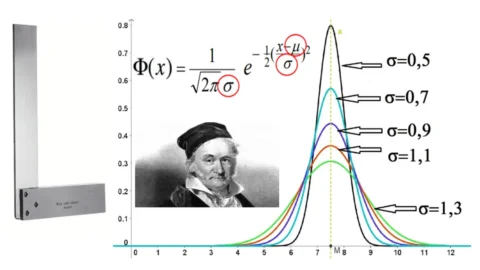
Oggi, la distribuzione normale è la distribuzione più importante ed utilizzata da chiunque abbia a che fare con un numero abbastanza grande di dati da classificare o interpretare. Come già accennato, il valore medio si trova esattamente al centro della distribuzione, così come mediana e moda. Allontanandosi da questi valori coincidenti, la curva si avvicina sempre più all’asse delle ascisse, ma non arriva mai a toccarlo (andamento asintotico). Nella sua formulazione generica più classica, la distribuzione normale descrive in realtà una famiglia di distribuzioni, tutte con la stessa forma caratteristica, ma con campane più o meno strette e appuntite oppure più larghe e piatte. Questi due fattori possono essere fatti variare utilizzando due soli parametri: il valor medio µ e lo scarto quadratico medio σ (o deviazione standard). Variando µ è possibile spostare orizzontalmente l’asse di simmetria della curva, variando σ, invece la curva si allarga (per valori maggiori) e si appiattisce (per valori minori). Per indicare che una variabile x si distribuisce come una normale si usa perciò scrivere X ~ N(µ,σ). Ad esempio, i valori prodotti da un processo di misura sono generalmente distribuiti normalmente, questo perché, misurando ripetutamente lo stesso oggetto, lo strumento non produce sempre lo stesso valore, ma piccole oscillazioni intorno al valore medio.
Quando una curva descrive una distribuzione di frequenze relative, l’area totale sottesa alla curva è pari a 1 (la somma delle frequenze relative). Dunque l’area a sinistra della media, in una distribuzione normale è pari a ½ (50% del totale), così come l’area alla sua destra. Quindi, quasi il 70% dell’area si trova compresa tra (x −σ) e (x +σ), ben il 95% si trova invece compresa tra (x − 2σ) e (x + 2σ) e addirittura il 99% si trova compresa tra (x − 3σ) e (x + 3σ). Questi σ (sigma) sono molto importanti per la gestione dei processi aziendali, poiché sono alla base di un programma di gestione della qualità che è stato elaborato proprio utilizzando la campana di Gauss per raggiungere il miglior controllo possibile sui processi. Introdotto per la prima volta dall’azienda di elettronica Motorola, nella seconda metà degli anni ottanta, aveva l’obiettivo di far sì che soltanto 3, al massimo 4 parti della produzione su un milione fossero difettose.
Questo sistema, ribattezzato “Six Sigma” proprio in virtù della capacità degli estremi (x − 6σ) e (x + 6σ) di garantire ben oltre il 99,99% della produzione funzionante, lasciando fuori solo lo 0,002% di produzione difettosa, ebbe talmente successo che si diffuse ad altre importanti compagnie, come General Electric, Toyota, Honeywell e Microsoft. Oggi, il metodo del 6σ, oltre a far parte del programma di studi di diversi percorsi didattici universitari, è alla base di una certificazione molto ambita dalla aziende e dai lavoratori.
Altri esempi di situazioni modellate da una distribuzione normale sono, come già introdotto, gli errori casuali nella misurazione di una grandezza fisica. L’errore può essere per eccesso o per difetto, quindi la variabile aleatoria dell’errore nella misura può assumere – in maniera simmetrica – valori positivi o negativi. L’errore tende a essere abbastanza piccolo, o meglio, errori più grandi sono meno probabili, quindi la curva decresce rapidamente man mano che ci si allontana dallo 0 (errore nullo), in entrambe le direzioni.
Chi si occupa di scienze demografiche sa perfettamente come, molte grandezze relative a una popolazione omogenea di persone, possano essere rappresentate da una distribuzione gaussiana, avente µ uguale al valore medio della grandezza nella popolazione. Statura, peso, indice di massa corporea, valori di pressione, glicemia e tante altre caratteristiche misurabili, hanno una distribuzione normale con µ e σ opportuni.
In un impianto di produzione in serie di parti di ricambio, la dimensione effettiva degli oggetti prodotti può, ad esempio, oscillare attorno al valor medio µ, che rappresenta la dimensione ottimale. L’obiettivo di chi si occupa della supervisione dei macchinari preposti alla produzione in serie, potrebbe essere quello di fare in modo che lo scarto quadratico medio σ sia il più piccolo possibile.
La Wechsler Adult Intelligence Scale (o WAIS) è il più noto test d’intelligenza utilizzato in età adulta ed è il test in base al quale è stato possibile, per la prima volta, avere punteggi standardizzati di QI (Quoziente Intellettivo), aventi media pari a 100 e scarto quadratico medio pari a 15. Ancora una volta siamo di fronte a grandezze che si distribuiscono lungo una curva a campana come quella di Gauss, che ci permettono di individuare un range di popolazione in base al QI. L’associazione internazionale del “Mensa”, ad esempio, è costituita da persone che abbiano raggiunto o superato il 98% della popolazione mondiale in base al proprio QI, ossia un punteggio maggiore di 130 proprio nel test di Wechsler. Questo significa che si tratta di solo il 2% della popolazione mondiale.
Gli esempi ulteriori che si possono fare sono davvero infiniti, ma di certo quelli proposti sono sufficienti per lasciarsi appassionare ad una cultura scientifica particolare, quella che riesce a vedere la bellezza nei modelli matematici, a farsi catturare dal fascino di un curioso mutuo adattamento – spontaneo – tra realtà e matematica, che quasi si riflette nella cultura umanistica dell’arte, quella dell’eleganza nella rappresentazione.